逻辑回归常用于处理二分类问题的,虽然也可以通过〚联合〛的方式处理多分类问题「有超过两个以上的类别」但这样比较麻烦。在处理多分类问题的时候我们可以使用softmax替代逻辑回归里的sigmoid激活函数,这样可以实现多分类操作。
Softmax函数
我们简单介绍一下Softmax函数,它的数学公式如下:
$$ \begin{align} y_i = \frac{e^{x_i}}{\sum_{j=1}^{n}e^{x_j}} \end{align} $$
当我们有一个数据 $x = \begin{bmatrix}x_1 & x_2 & x_3\end{bmatrix}$ 输入到softmax,它会输出的 $y$ 值将如下:
$$ y = \begin{bmatrix}y_1 & y_2 & y_3\end{bmatrix} \ \Leftrightarrow\ \left\{ \begin{align} y_1 = \frac{e^{x_1}}{\sum_{j=1}^{n}e^{x_j}} \\ y_2 = \frac{e^{x_2}}{\sum_{j=1}^{n}e^{x_j}} \\ y_3 = \frac{e^{x_3}}{\sum_{j=1}^{n}e^{x_j}} \\ \end{align} \right. $$
我们用一个具体的数值来演示一下,假设输入数据如下:
$$ x = \begin{bmatrix}0 & 1 & 2\end{bmatrix} $$
于是计算过程如下:
$$ \begin{align} \sum_{j=1}^{3}e^{x_j} &= e^0 + e^1 + e^2 \\ &= 1 + 2.71828183 + 7.3890561 \\ &= 11.107337927389695 \\ y_1 &= \frac{e^{x_1}}{\sum_{j=1}^{3}e^{x_j}} = 0.09003057 \\ y_2 &= \frac{e^{x_2}}{\sum_{j=1}^{3}e^{x_j}} = 0.24472847 \\ y_3 &= \frac{e^{x_3}}{\sum_{j=1}^{3}e^{x_j}} = 0.66524096 \\ \end{align} $$
最终输出y为:
$$ y = \begin{bmatrix}0.09003057 & 0.24472847 & 0.66524096\end{bmatrix} $$
y的每一个元素的值会落在0到1之间,并且将y的每一个元素值相加会得到数值1,因此softmax的输出常常用于代表各个类别的概率,例如当第一个元素的值为0.09003057时代表有9.003057%的可能性为第一个类别;第二个元素的值为0.24472847代表有24.472847%的可能性为第二个类别……以此类推。
引入所需的模块
import matplotlib.pyplot as plt
import torch
torch.manual_seed(7)
import torch.nn.functional as F
torch.manual_seed(7)将pytorch的随机生成器的种子固定在7,这样可以让每一次运行的结果相同。
由于我们需要绘制图像,所以除了引入pytorch我们还引入了matplotlib;torch.nn.functional包含pytorch中大量的神经网络相关的函数,我们将用到它。
构建输入输出
我们随机产生一个10x5的矩阵X作为输入,它的每一行为一个数据点,共计10个数据点。
除此之外,我们还创建了一个索引index,它的生成方法是: 将矩阵X与另一个5x3的随机矩阵相乘得到一个10x3的新矩阵,然后取这个新矩阵中每一行的最大值元素的下标。
X = torch.randn((10, 5), dtype=torch.float32)
index = torch.argmax(X @ torch.randn((5, 3), dtype=torch.float32), dim=1)
print('index:')
print(index)
我们还需要使用one-hot函数将索引index进行转换,让它变成一个元素值为0或1的10x3矩阵,该矩阵的每一行只有一个1,并且第n行中值为1的元素的下标等于索引index第n行的元素值,即有: T[n, index[n]]的值为1:
T = F.one_hot(index, 3).type(torch.float32)
print('one hot:')
print(T)
设置需要拟合的参数
由于我们的输出是个nx3的矩阵所以权重W的维度是5x3,偏置b的维度是3:
W = torch.ones((5, 3), dtype=torch.float32, requires_grad=True)
b = torch.zeros((3, ), dtype=torch.float32, requires_grad=True)
正向传播
在一个for循环中执行正向传播代码:
steps = 100
losses = []
print('training...')
for step in range(steps):
A = X @ W + b
P = torch.softmax(A, dim=1)
loss = F.cross_entropy(P, T)
losses.append(loss.item())
i = step + 1
if i % 10 == 0:
print(f'step: {i}/{steps}, loss={losses[-1]}')
torch.softmax(A, dim=1)调用softmax激活函数需要指定维度dim=1这是因为矩阵A的每一行对应一个数据点,我们需要单独给每一行进行softmax。由于使用的是softmax激活函数,因此我们的损失函数需要采用交叉熵损失函数即F.cross_entropy,该函数的第一个参数为softmax的输出,第二个参数为正确的分类标识。
我们使用列表losses存储每一轮的损失值loss.item(),并每10个循环打印输出一次。
反向传播
调用loss.backward()进行反向传播用以求解W与b的梯度,然后在不计算梯度的模式下进行更新:
loss.backward()
lr = 0.1
with torch.no_grad():
W -= lr * W.grad
b -= lr * b.grad
W.grad.data.zero_()
b.grad.data.zero_()
查看拟合效果
打印输出矩阵P,矩阵P的每一行的数值处于0到1之间,代表改行所对应的数据点在某个类别上的概率。例如: P的第0行的0个元素为0.2115则表示第0个数据点属于第0个类别的概率为21.15%,我们可以调用torch.argmax(P, dim=1)将矩阵P转换成类似index的索引向量:
print('probabilities:')
print(P.detach())
print('true:', index)
with torch.no_grad():
print('pred:', torch.argmax(P, dim=1))
运行后输出:
probabilities:
tensor([[0.2115, 0.7491, 0.0394],
[0.1779, 0.0743, 0.7478],
[0.2192, 0.4239, 0.3569],
[0.0591, 0.0165, 0.9244],
[0.0901, 0.7963, 0.1136],
[0.9610, 0.0273, 0.0117],
[0.7126, 0.1436, 0.1438],
[0.9565, 0.0049, 0.0386],
[0.9441, 0.0457, 0.0102],
[0.1677, 0.4086, 0.4237]])
true: tensor([1, 2, 1, 2, 1, 0, 0, 0, 0, 2])
pred: tensor([1, 2, 1, 2, 1, 0, 0, 0, 0, 2])
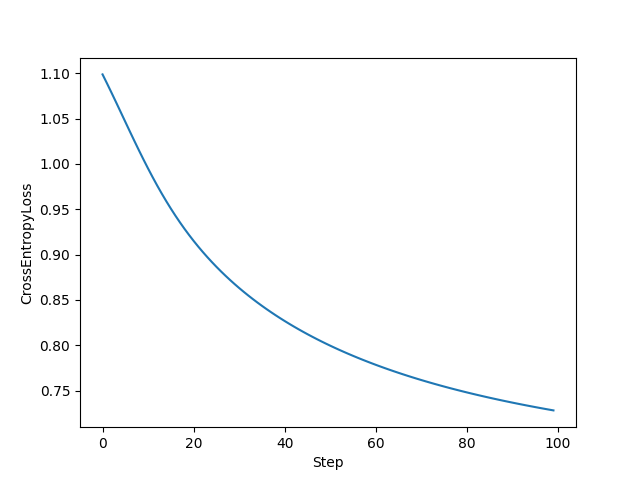
绘制拟合过程中的损失率
最后我们还可以可视化一下拟合过程中损失率的变化:
plt.xlabel('Step')
plt.ylabel('CrossEntropyLoss')
plt.plot(range(len(losses)), losses, '-')
plt.show()
完整代码
import matplotlib.pyplot as plt
import torch
torch.manual_seed(7)
import torch.nn.functional as F
X = torch.randn((10, 5), dtype=torch.float32)
index = torch.argmax(X @ torch.randn((5, 3), dtype=torch.float32), dim=1)
print('index:')
print(index)
T = F.one_hot(index, 3).type(torch.float32)
print('one hot:')
print(T)
W = torch.ones((5, 3), dtype=torch.float32, requires_grad=True)
b = torch.zeros((3, ), dtype=torch.float32, requires_grad=True)
steps = 100
losses = []
print('training...')
for step in range(steps):
A = X @ W + b
P = torch.softmax(A, dim=1)
loss = F.cross_entropy(P, T)
losses.append(loss.item())
i = step + 1
if i % 10 == 0:
print(f'step: {i}/{steps}, loss={losses[-1]}')
loss.backward()
lr = 0.1
with torch.no_grad():
W -= lr * W.grad
b -= lr * b.grad
W.grad.data.zero_()
b.grad.data.zero_()
print('probabilities:')
print(P.detach())
print('true:', index)
with torch.no_grad():
print('pred:', torch.argmax(P, dim=1))
plt.xlabel('Step')
plt.ylabel('CrossEntropyLoss')
plt.plot(range(len(losses)), losses, '-')
plt.show()