由于本章的后部分内容需要使用到一点关于矩阵运算的基础操作,所以我们在这里先了解一下。
创建矩阵
import numpy as np
m = np.matrix([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
])
print(m)
使用np.matrix函数可以创建一个numpy矩阵,该函数可以像np.array一样接收python的列表对象来设置矩阵的值。
除了从python列表创建矩阵,还可以从python数组以及矩阵中创建矩阵,正如下面这样:
m2 = np.matrix(np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]))
print(m2)
m3 = np.matrix(np.matrix([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]))
print(m3)
另外,np.matrix还具有一种参数形式:
m4 = np.matrix('1 2 3; 4 5 6; 7 8 9')
print(m4)
用一个字符串初始矩阵的元素值,每一行元素之间用;进行分隔,每行的各个元素用空格进行分隔,类似matlab或octave的矩阵创建形式。
矩阵转置
可以使用矩阵转置的方法将矩阵的行和列的关系对调,在numpy当中可以通过矩阵的属性Matrix.T实现:
m = np.matrix([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
])
print(m)
mT = m.T
print(mT)
运行后输出结果:
[[1 2 3]
[4 5 6]
[7 8 9]]
[[1 4 7]
[2 5 8]
[3 6 9]]
加法减法除法运算
直接使用运算符+、-、/进行的运算都是对应元素间两两运算后的结果:
m = np.matrix([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
])
print(m)
print(m + m)
print(m - m)
print(m / m)
运行后输出结果:
[[1 2 3]
[4 5 6]
[7 8 9]]
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]
[[0 0 0]
[0 0 0]
[0 0 0]]
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
矩阵乘法与对应元素的乘法
直接使用运算符*会对matrix对象调用numpy的矩阵乘法,矩阵乘法的规则如下图所示:
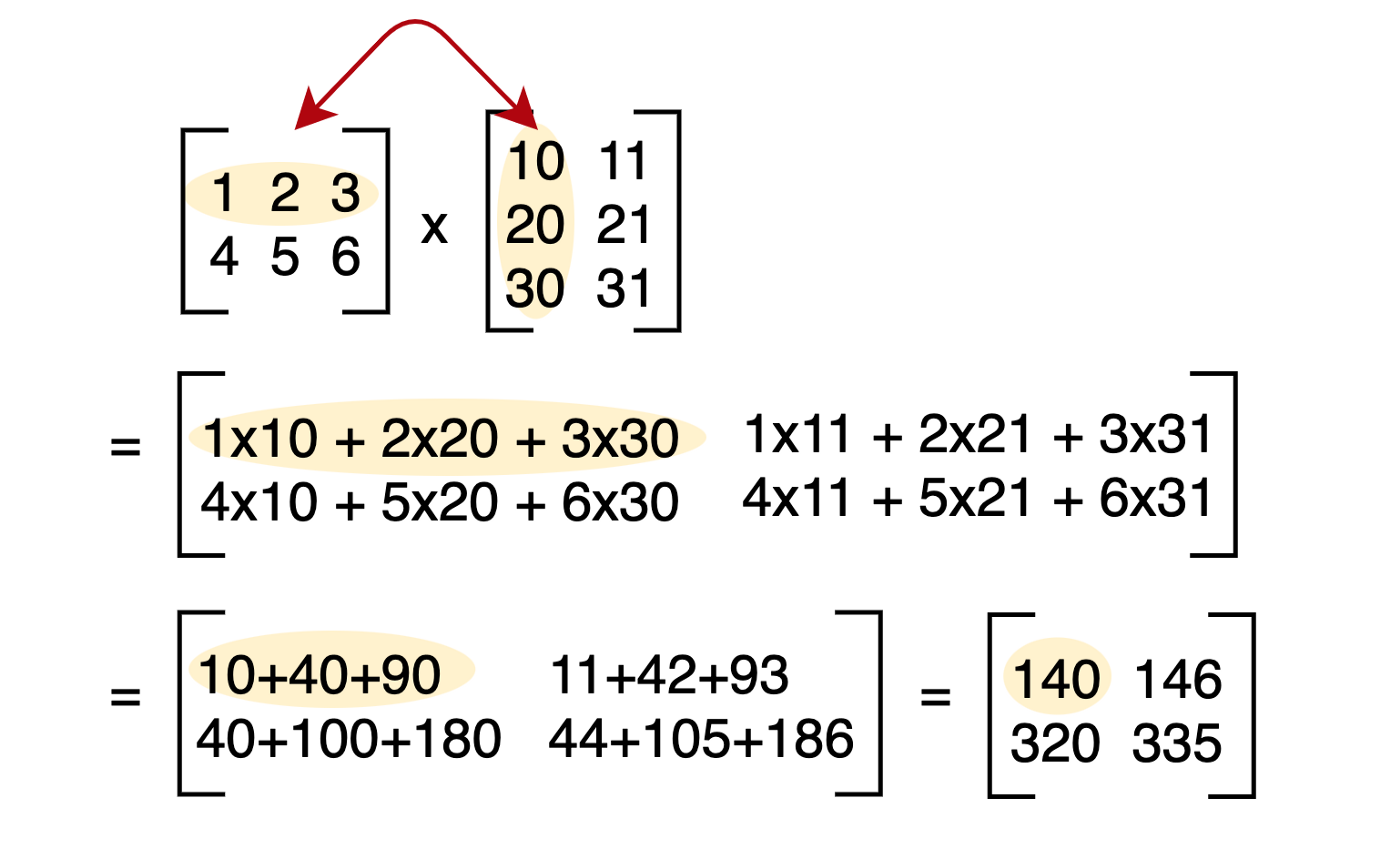
如果想要计算对应元素相乘后的结果可以调用函数np.multiply进行计算:
m = np.matrix([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
])
print(m)
print(m * m)
print(np.multiply(m, m))
运行后输出结果:
[[1 2 3]
[4 5 6]
[7 8 9]]
[[ 30 36 42]
[ 66 81 96]
[102 126 150]]
[[ 1 4 9]
[16 25 36]
[49 64 81]]
矩阵的索引
numpy的矩阵对象和数组对象一样可以进行索引。
获取矩阵的某行或某几行:
print(m[0])
print(m[1:3])
获取矩阵的某列或某几列:
print(m[:, 0])
print(m[:, 1:3])
其它复杂的索引可以参考对numpy数组对象的索引方式。